Page 2 of 6
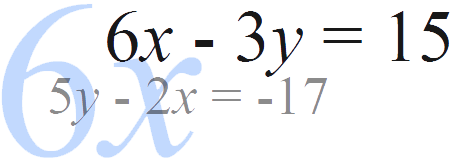
The equations in question 1 all have the same coefficients for either \(x\) or \(y\). One of these variables can be eliminated by simply adding or subtracting the equations. Solve the following equations:
Question 1
| (a) | \( 2x + y = 10\) | (b) | \( x + 8y = 55\) | (c) | \( 3x - 4y = 4\) | (d) | \( 7x - 3y = 66\) |
| \( 2x + 4y = 22\) | \( x - 3y = -11\) | \( 2x + 4y = 36\) | \( 2x - 3y = 21\) | ||||
| (e) | \( 7x - 6y = 10\) | (f) | \( 5x + 2y = 29\) | (g) | \( 4x + 2y = -2\) | (h) | \( 6x - 4y = -13\) |
| \( 4x - 6y = -2\) | \( 3x - 2y = 11\) | \( 7x + 2y = 4\) | \( 6x + 2y = 11\) | ||||
| (i) | \( 3x + 5y = 41\) | (j) | \( 12x +12y = -3\) | (k) | \( 5x + 8y = 51\) | (l) | \( 8x + 4y = 3\) |
| \( x + 5y = 37\) | \( 2x -12y = -4\) | \( 2x - 8y = -30\) | \( 8x + 6y = 2\) | ||||
