Page 3 of 6
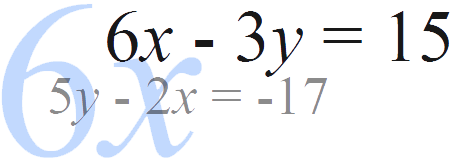
Multiply one equation to make the number of \(x\)'s or \(y\)'s the same. Then add or subtract the equations to eliminate either \(x\) or \(y\). Solve the following equations:
Question 2
| (a) | \( 2x + y = 11\) | (b) | \( 6x + 5y = 8\) | (c) | \( 3x + 2y = 8\) | (d) | \( 4x - 3y = 15\) |
| \( 4x + 8y = 52\) | \( 3x + 3y = 6\) | \( 6x + 5y = 17\) | \( 2x - 6y = 12\) | ||||
| (e) | \( 12x - 3y = -6\) | (f) | \( 6x + 2y = 3\) | (g) | \( 4x + 5y = 12\) | (h) | \( 2x + 5y = 11\) |
| \( 4y - 4x = 11\) | \( 10x - 10y = -3\) | \( 2x - 6y = 40\) | \( 4y - 2x = 7\) | ||||
| (i) | \( 8x + 4y = -2\) | (j) | \( x + 7y = 33\) | (k) | \( 10x + 6y = -22\) | (l) | \( 3x - 4y = 1\) |
| \( 4x - 2y = 7\) | \( 2x - 3y = -19\) | \( 5x - 3y = 19\) | \( 4x + 8y = -4\) | ||||
